The USS Enterprise drops out of warp and slips into a parking orbit around an uncharted alien planet. The good Captain orders a scan for lifesigns, and within seconds he is being informed exactly what lifeforms are present, including the preindustrial tribes of humanoids on the southern continent. How feasible is this really? Well, unfortunately for Star Trek fans, identifying a species from orbit will perhaps forever remain in the realm of science fiction. For astrobiologists, however, revealing the presence of life on a remote planet is becoming possible even now, on 21st century Earth. Within a decade there will be telescopes capable of detecting the chemical fingerprints of life on planets nearly 50 light years away. And within out lifetimes there may even be telescopes able to image the oceans and continents of alien worlds.
Author: lewis
Alan Turing is considered to be one of the most brilliant mathematicians of the last century. He helped crack the German Enigma code during the Second World War and laid the foundations for the digital computer. His only foray into mathematical biology produced a paper so insightful that it is still regularly cited today, over 50 years since it was published. In it he described how a set of ‘reaction-diffusion equations’ explain how the wonderful diversity of animal patterns may be generated.
Read full article on +plus
This article has been reprinted in Muse, the YouthAgency magazine. The agency is run by the National Association for Gifted Children and aims to inspire able students to cultivate their abilities. pdf copy of the reprint.
Categories
Practice Makes Perfect
As we saw in the last edition of +plus, mathematical techniques have been applied very successfully to analysing certain types of games. The two examples that we looked at were the simple subtraction game Nim, and the much more complex case of chess endgames. The next step is to see how computers, which are no more than automated maths machines, are being programmed to actually play chess themselves. It is theoretically possible to play chess perfectly, but neither humans nor machines will probably ever accomplish this. Computers have, however, already practically achieved perfection in draughts, and soon may be said to have ‘solved’ the game.
This is the report of my MRes short project.
Supervisors: Andy Anderson, Alan Johnston, Peter McOwan
Categories
Games People Play
Mathematicians love games. Not only can they have fun while looking like they’re busy working, but even the simplest games can demand clever tactics and strategies to win. These are the perfect kinds of problems for solving with maths.
One branch of mathematics, called Combinatorial Game Theory, was developed around 30 years ago specifically to deal with the analysis of games. It prescribes a way of breaking games down into smaller parts that are easier to examine, and then using a special kind of algebra to add up the values of the individual subgames. And if there’s one thing that mathematicians are good at it’s counting.
Read full article on +plus
The ambitious project of sequencing the DNA in the human genome released its first draft three years ago. At the time it was often portrayed as `reading the book of life’, but what is only recently being understood is how appropriate this metaphor really is. The jargon of molecular biology is scattered with terms borrowed from linguistics, such as transcribe, translate and code. The parallels between these two fields run much deeper than this though, and it has been discovered that both DNA and the proteins that it codes for have a grammatical structure like language. This has lead to the very productive swapping of ideas and techniques between biologists and linguists. For example, `authorship tests’ have been applied to unknown DNA sequences and `evolutionary trees’ have been constructed of old texts. But first, in what ways are DNA and proteins so profoundly similar to language?
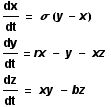The Lorenz equations are a set of three coupled non-linear ordinary differential equations (ODE). They make up a simplified system describing the two-dimensional flow of a fluid. As can be seen, the derivative of all three variables is given with respect to t, and as a function involving one or both of the other variables (thus they are said to be coupled). The usual values taken by the parameters are as follows:
sigma = 10, r = 28, and b = 8/3.
As time is incremented then, the calculated values of x, y, z change as shown in the timeseries plot below. x = red, y = green, z = blue.
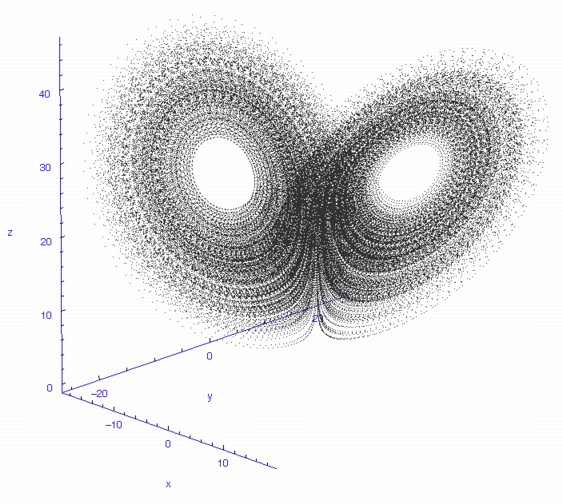
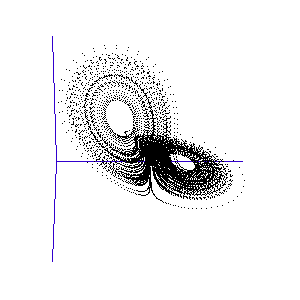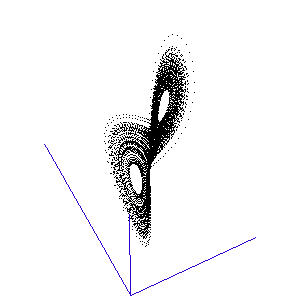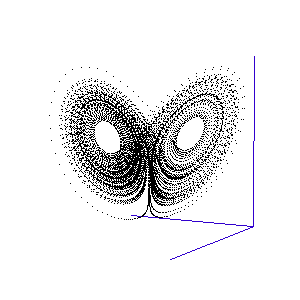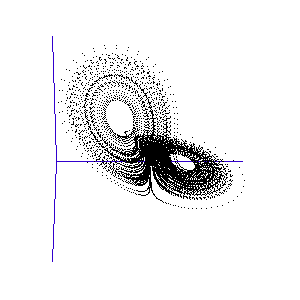
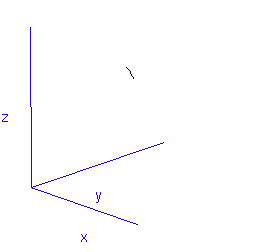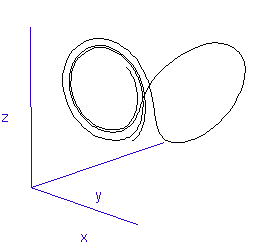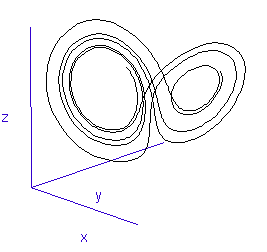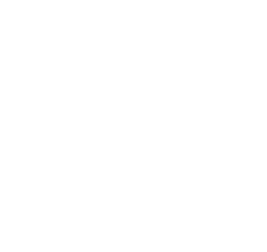The fluctuations are seemingly utterly random. More structure can be seen, however, if the same timeseries is plotted as a sequence of co-ordinates describing a trajectory through 3-space. As shown to the right, the surface resembles a twisted bow-tie. It is known as the Lorenz strange attractor, and no equilibrium (dynamic or static) is ever reached – it does not form limit cycles or achieve a steady state. Thus, no trajectory ever coincides with any other. Instead, it is an example of deterministic chaos, one of the first realised by mathematicians.
One of the properties of a chaotic system is that it is sensitive to initial conditions. This means that no matter how close two different initial states are (i.e. even down to the 20th decimal place) their trajectories will soon diverge. This is popularly referred to as the “Butterfly Effect”, whereby small changes in the initial state can lead to rapid and dramatic differences in the outcome. The metaphor is that a butterfly flapping its wings in Brazil could result in a tornado in Texas.
The Lorenz equations cannot be solved analytically by integration. Instead, a numerical approximation technique must be used. The 4th order Runge-Kutta (RK) method employed here takes a weighted average of four estimates of the derivative at a point in order to calculate the new position after a time increment. The lower-order error terms cancel out, making RK very robust despite its simplicity.
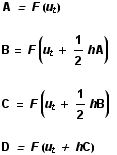To generate all of these images and animations, a Mathematica programme was written to perform the RK numerical analysis of the Lorenz equations. For the initial state, an arbitrary point in 3-space, ut , is chosen, and then four derivatives calculated (A, B, C and D) using a time increment of h. In each case, F is the three-dimensional vector function composed of the Lorenz differential equations given above. These derivatives are weighted and combined to give the approximation for the next point, ut+h .
The three components of this point are appended to a storage list, and then the whole calculation reiterated a large number of times. For the high resolution image above, 100,000 co-ordinates were calculated and plotted, expending almost an hour of computer runtime. For the animation below, only 10,000 points were used.
Once calculated, all of the points in this data list are plotted in order to visualise the Lorenz attractor. This draw command was placed in a programme loop, with the x, y, and z co-ordiantes of the viewing-point for the projection incremented each time to generate a string of images. These were then converted into an animated .gif to create the rotating attractor shown to the left.
The animation of the trajectory through time (shown at the top) was created by calculating just 1,000 co-ordinates, starting with a point known to be near the transition region between the two lobes. Only a subset of these points were plotted each time in the draw loop, beginning with the first 5, then the first 10, first 15, 20, 25, and so on.
Recent genetic research has answered some long-running questions about the ancient origins of the humble cow. At the time when the first civilisations were being born great floods of cattle surged across the continents. The results of these prehistoric migrations may now help save modern European herds.
The humpback whale, Megaptera novaeangliae, produces the most complex vocalisations of all 77 cetacean species, which have been dubbed by Payne and MacVay (1971) as “songs”. These songs are hierarchical in nature, with rules seemingly governing their organisation and evolution over breeding seasons. No one hypothesis of the song’s function adequately explains its complexity and structure, except perhaps for the theory that it constitutes the first non-human language yet discovered. Buck and Suzuki (1999) have applied Information theory to analyse a sample of humpback song converted into a stream of symbols using a self-organising neural network (SONN). This theory can be used to determine the maximum amount of information contained within a coded sequence by the unpredictability of the next symbol. Different assumptions can be made about the nature of the sequence; the next symbol is randomly determined (thus no hierarchical structure is possible within the sequence), or the probability of the next symbol is dependent on the previous one, or two symbols (0th, 1st and 2nd Order Markov models respectively). It was found that a first-order assumption could not reasonably model humpback song, meaning that humpback song possesses a hierarchical structure suggestive of language. The low rate of information transmission, about 0.1 – 0.6 bits per second, may ensure reliable communication over long distances in noisy, unpredictable acoustic conditions.
The suborder Microchiroptera contains approximately 800 species of bats with a sophisticated biosonar system used to actively interrogate the local environment and analyse the retuned echoes to extract information on obstacles and potential prey in the flight path. Most are insectivorous and hunt with aerial-hawking or gleaning tactics, although some, such as Noctilio leporinus, predate on fish and use echolocation to detect localised surface ripples. Much research has been conducted into the neurophysiology of echolocation with its superb acoustic discrimination capabilities, including very fine temporal and frequency resolution. This review covers firstly bat call design and hunting behaviour, and the neural basis of their capabilities. The second half deals with the question of a bat-moth co-evolutionary arms race.
Categories
A Walk on the Wild Side
Lewis Dartnell dons his naturalist hat and ventures into the Amazonian rainforest of Eastern Equador
Two years ago I’d formed the somewhat misconceived notion that travelling could never amount to anything more than a GAP year of one of three expensive and clichéd models: booze & bifta fuelled tour of East coast Australia, pestering Gurus with mind to “discovering myself” or scouring the Lonely Planet Guide to Kenya for that one extra shrink-wrapped Experience that would distinguish me as a traveller. It seemed to me Tourist is to backpacker as MacBeth is to thesp, and Alex Garland’s Lord of the Flies “Beach” was doing no good in convincing me that this was my copa de mate. After two years of trying to equate Paddington delays to the travelling tales of friends in the Kings Arms, however, I decided that enough was enough and it was time to broaden my horizons.