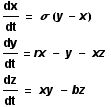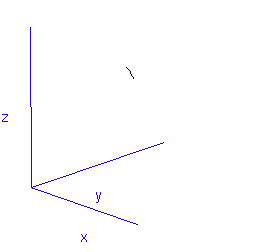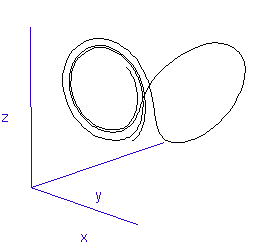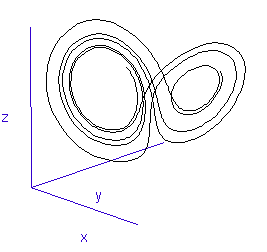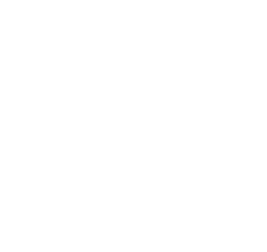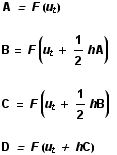Category: Postgraduate

Postgraduate

 

After graduating from my Biology degree at Oxford I moved to University College London for a combined MRes-PhD programme in the deeply interdisciplinary CoMPLEX (Centre for Mathematics & Physics in the Life Sciences and Experimental Biology).

MRes

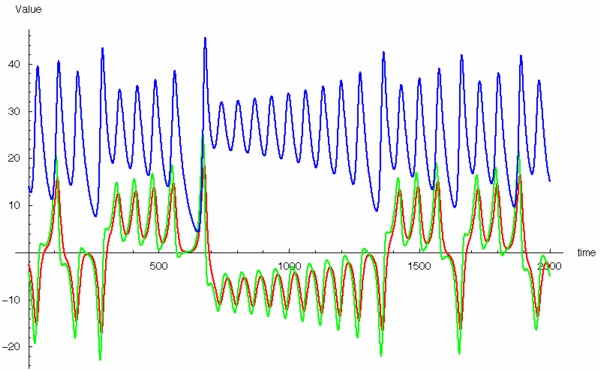
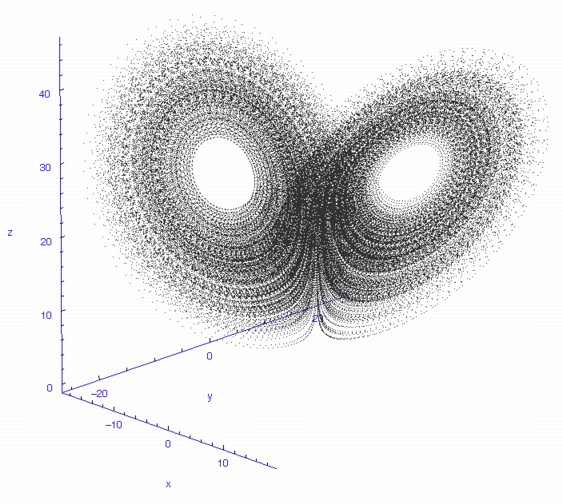
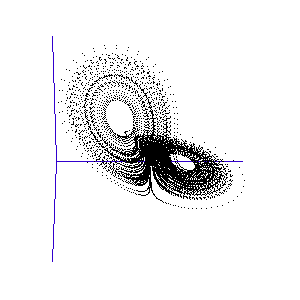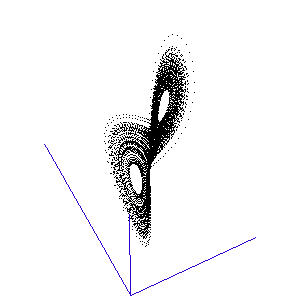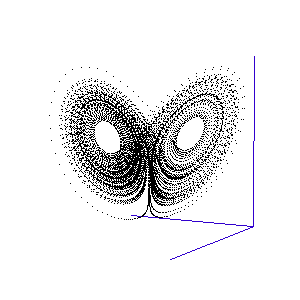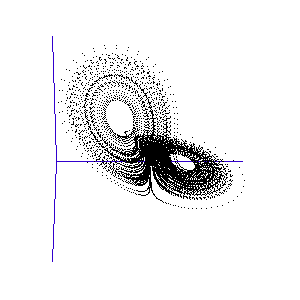
Lorenz_anim_small

During the first year, the MRes (Master of Research), I was exposed to an enormous amount of physics and instrumentation, as well as mathematical modelling and computational approaches. During this MRes I worked on several small projects, including one on the numerical modelling of chaotic systems – see Runge-Kutta and the Lorenz Attractor – and I published my first paper, on my analysis of the connection architecture of the network of interacting genes that guards our cells against turning cancerous – Robustness of the p53 network and biological hackers (see my bibliography for a downloadable pdf).

Anim_6

 

I also worked on a class of optical illusions that disrupt the accurate perception of movement, called motion illusions, that I believed to be linked to a particular display exhibited by cuttlefish. The write-up of this, complete with animations of the motion illusions is available as Motion illusions & active camouflaging.

My major research project for the MRes continued my preliminary work on motion illusions, and a pdf of the final report is available as  Illusions disrupting the accurate perception of velocity and position.

 

 PhD

ModelAfter completing the MRes year, CoMPLEX offers the phenomenal opportunity of being able to chose your own PhD project on the interfaces of biology and approach your own potential supervisors, already fully-funded. I took this chance to move into the  field of astrobiology and the search for life beyond Earth. Supervised by Andrew Coates (Mullard Space Sciences Laboratory) and John Ward (Microbiology) I devised an interdisciplinary research project combining computer modelling of the high energy particle physics of cosmic rays and irradiation experiments of extremophile bacteria I isolated from the Dry Valleys in Antarctica, submitting my thesis in 2007. I published a number of papers from this PhD work and my thesis has since been republished by the academic publishers as ‘Martian Death Rays‘. The abstract of my thesis is:

 

Any microbial life extant in the top meters of the martian subsurface is likely to be held dormant for long periods of time by the current permafrost conditions. In this potential habitable zone, a major environmental hazard is the ionising radiation field generated by the flux of exogenous energetic particles: solar energetic protons and galactic cosmic rays. The research reported here constitutes the first multidisciplinary approach to assessing the astrobiological impact of this radiation on Mars.

A sophisticated computer model has been constructed de novo to characterise this complex subsurface ionising radiation field and explore the influence of variation in crucial parameters such as atmospheric density, surface composition, and primary radiation spectra. Microbiological work has been conducted to isolate novel cold-tolerant bacterial strains from the Dry Valleys environment of Antarctica, an analogue site to the martian surface, and determine their phylogenetic diversity and survival under high-dose gamma-ray exposure frozen at -79◦C, a temperature characteristic of the martian mid-latitude permafrost.

Original results are presented pertinent to microbial survival time, persistence of organic biomarkers, and calibration of the optically stimulated luminescence dating technique, as a function of depth. The model predicts a population of radiation resistant cells to survive in martian per- mafrost soil for 450,000 years at 2 m depth, the proposed drill length of the ExoMars rover. The Antarctic culturing studies identified representatives of four bacterial genera. The novel isolate Brevundimonas sp. MV.7 is found to show 99% 16S sequence similarity to cells discovered in NASA spacecraft assembly clean rooms, with the experimental irradiation determining this strain to suffer 10−6 population inactivation after a radiation dose of 7.5 kGy in martian permafrost conditions. Integrating the modelling and experimental irradiation, this research finds a contaminant population of such cells deposited just beneath the martian surface would survive the ambient cosmic radiation field for 117,000 years.

Comments Off on Postgraduate Posted in

Space bugs!

Space_bugsOn Earth, microbes get absolutely everywhere. Indeed, there seem to be very few completely sterile natural environments. But what about microbial colonization of locations beyond Earth? In this article we’ll explore the realm of space bugs. There is a great deal of interest in the microbiology of the closed artificial environments created for human exploration of the cosmos, such as the International Space Station (ISS), as well as in minimizing the risks of inadvertently transporting terrestrial contamination elsewhere, and even the possibility of a natural mechanism spraying life between worlds over the history of the solar system.

Download pdf

Runge-Kutta and the Lorenz Attractor

Lorenz_eqThe Lorenz equations are a set of three coupled non-linear ordinary differential equations (ODE). They make up a simplified system describing the two-dimensional flow of a fluid. As can be seen, the derivative of all three variables is given with respect to t, and as a function involving one or both of the other variables (thus they are said to be coupled). The usual values taken by the parameters are as follows:

sigma = 10, r = 28, and b = 8/3.

As time is incremented then, the calculated values of x, y, z change as shown in the timeseries plot below. x = red, y = green, z = blue.

xyz_timeseries

Lorenz_timeseriesThe fluctuations are seemingly utterly random. More structure can be seen, however, if the same timeseries is plotted as a sequence of co-ordinates describing a trajectory through 3-space. As shown to the right, the surface resembles a twisted bow-tie. It is known as the Lorenz strange attractor, and no equilibrium (dynamic or static) is ever reached – it does not form limit cycles or achieve a steady state. Thus, no trajectory ever coincides with any other. Instead, it is an example of deterministic chaos, one of the first realised by mathematicians.

One of the properties of a chaotic system is that it is sensitive to initial conditions. This means that no matter how close two different initial states are (i.e. even down to the 20th decimal place) their trajectories will soon diverge. This is popularly referred to as the “Butterfly Effect”, whereby small changes in the initial state can lead to rapid and dramatic differences in the outcome. The metaphor is that a butterfly flapping its wings in Brazil could result in a tornado in Texas.

Lorenz_big

The Lorenz equations cannot be solved analytically by integration. Instead, a numerical approximation technique must be used. The 4th order Runge-Kutta (RK) method employed here takes a weighted average of four estimates of the derivative at a point in order to calculate the new position after a time increment. The lower-order error terms cancel out, making RK very robust despite its simplicity.

Runge-Kutta1To generate all of these images and animations, a Mathematica programme was written to perform the RK numerical analysis of the Lorenz equations. For the initial state, an arbitrary point in 3-space, ut , is chosen, and then four derivatives calculated (A, B, C and D) using a time increment of h. In each case, F is the three-dimensional vector function composed of the Lorenz differential equations given above. These derivatives are weighted and combined to give the approximation for the next point, ut+h .

Runge-Kutta2

 

The three components of this point are appended to a storage list, and then the whole calculation reiterated a large number of times. For the high resolution image above, 100,000 co-ordinates were calculated and plotted, expending almost an hour of computer runtime. For the animation below, only 10,000 points were used.

Lorenz_animOnce calculated, all of the points in this data list are plotted in order to visualise the Lorenz attractor. This draw command was placed in a programme loop, with the x, y, and z co-ordiantes of the viewing-point for the projection incremented each time to generate a string of images. These were then converted into an animated .gif to create the rotating attractor shown to the left.

The animation of the trajectory through time (shown at the top) was created by calculating just 1,000 co-ordinates, starting with a point known to be near the transition region between the two lobes. Only a subset of these points were plotted each time in the draw loop, beginning with the first 5, then the first 10, first 15, 20, 25, and so on.